Finite Element Method

In the field of agricultural sciences, numerical modelling has proven to be a valuable tool in finding solutions to practical and scientific issues. Such models are necessary to understand the structure related properties of plants, like fruits and vegetables, and bring, in the next step, possibilities of extension by nano-structural features (like cell wall composition). This knowledge will be useful for engineering and improve fruits and vegetables quality.

The basic idea behind finite element method (FEM) is subdivision of a spatial domain of the problem into a simpler parts called the finite elements. The solution in global domain is obtained as a result of assembly of local solutions for the finite elements. Finite element method allows studies of systems with large complexity, irregular shapes and nonhomogeneous material properties.

Studies carried out by the Interdepartmental Laboratory of Numerical Modeling are aimed to create computational models of plant tissues at different spatial scales.

Modelling of plant tissues mechanical properties

Physical properties plant materials are related to several micro- and macroscopic morphological features such as the spatial arrangement and shape of cells, the number of intercellular spaces, turgor, the nano-composition of cell walls and the degree of degradation of the middle lamellae. The experimental analysis of the structure related micromechanical properties of plants  has been constrained by the lack of technology available for conducting reliable measurements at such scales. Deeper understanding of mechanical properties of plant tissues can be achieved by means of the numerical models of tissue deformation under various load conditions.

Up to now, the majority of models described in the literature was based on the principles of classical continuum mechanics. Most often, tissues were described by empirical or analytical models, as uniformly stressed structures, with symmetry and uniformity assumptions on cell shape and cell wall deformations. Although this approach allowed for fairly accurate predictions of the behavior of the plant materials in engineering applications, it was unable to provide an explanation of the micro-scale mechanisms underlying deformation and failure of tissue.

The research was co-founded by National Science Centre of Poland (research grant no. 2011/01/N/NZ9/02496).

Tissue structure modelling

One of the important steps in solving a problem, before the appropriate analysis with FEM, is to create a virtual model of the tested object. The virtual model is defined by its geometry, material properties and boundary conditions such as loads and the type of supports. It is important to create a proper model with the highest possible degree of accuracy regarding real shape reconstruction; but on the other hand, the model must be simple enough to allow for efficient calculations.

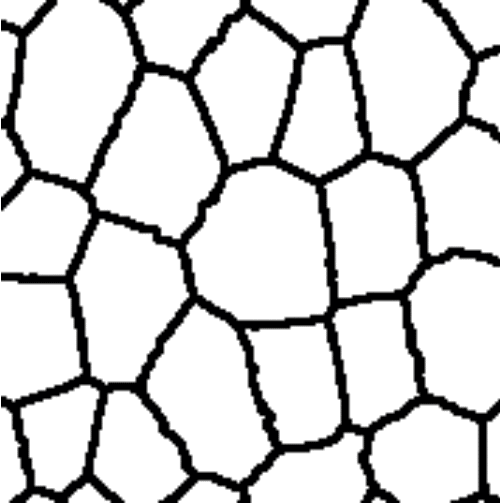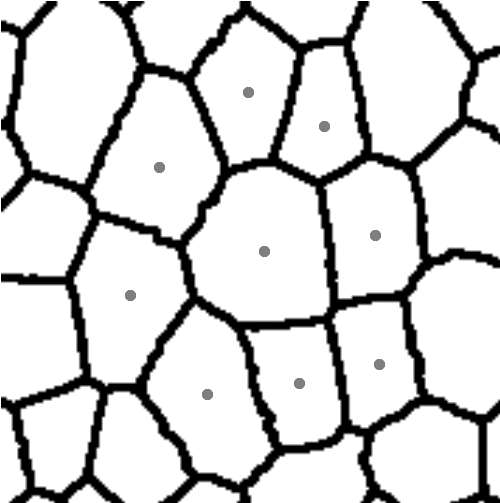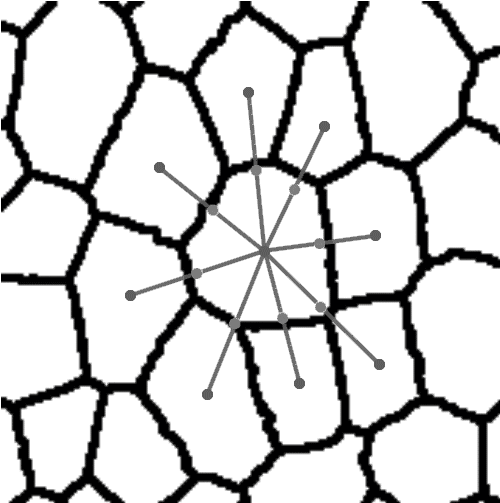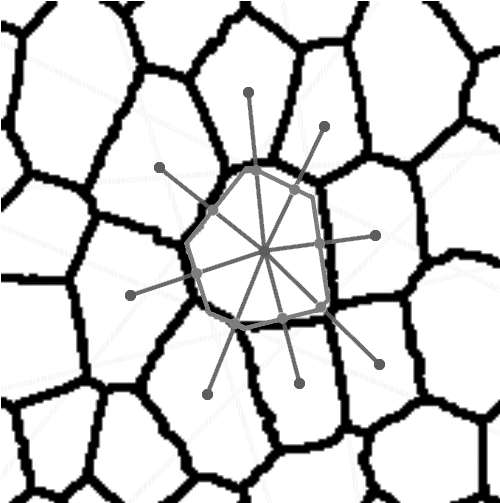
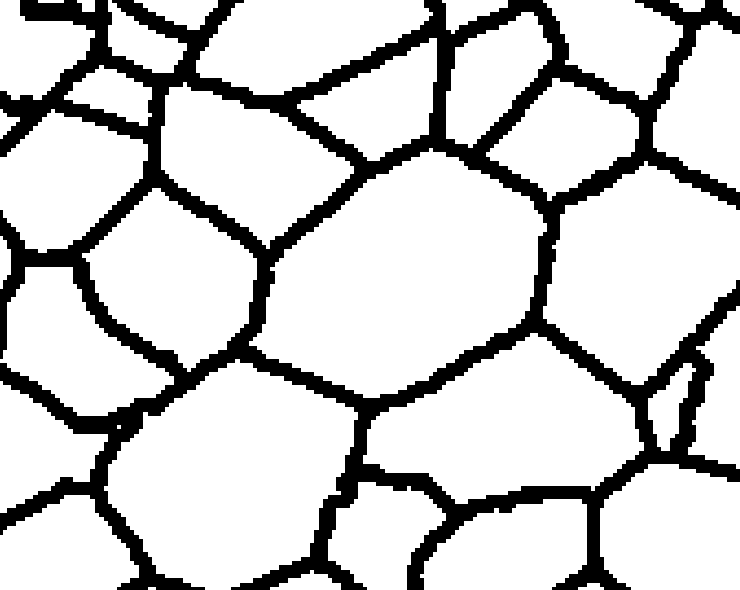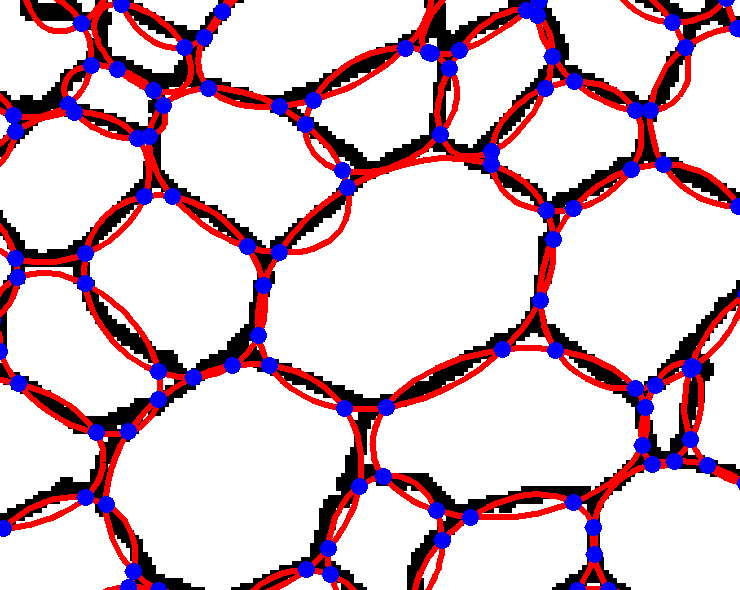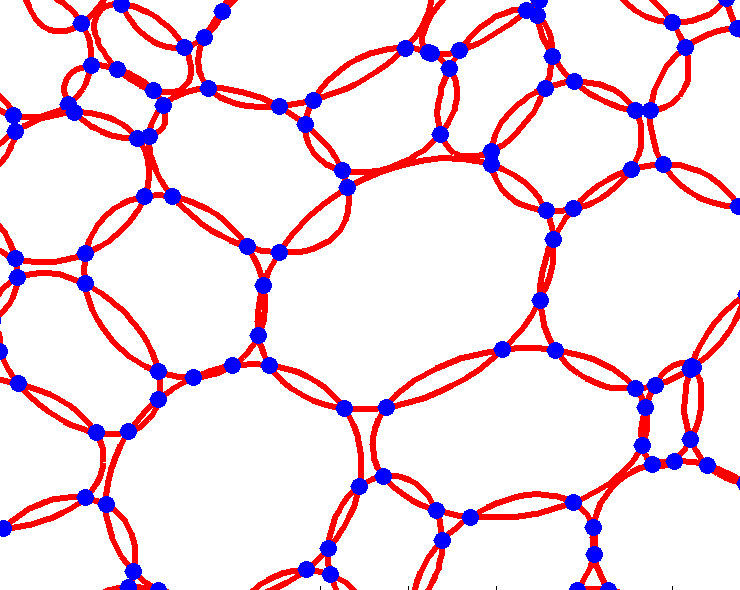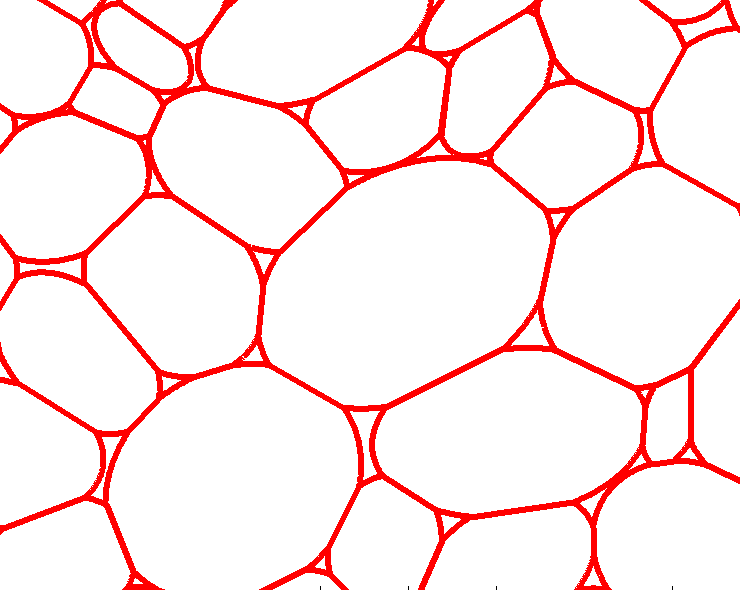
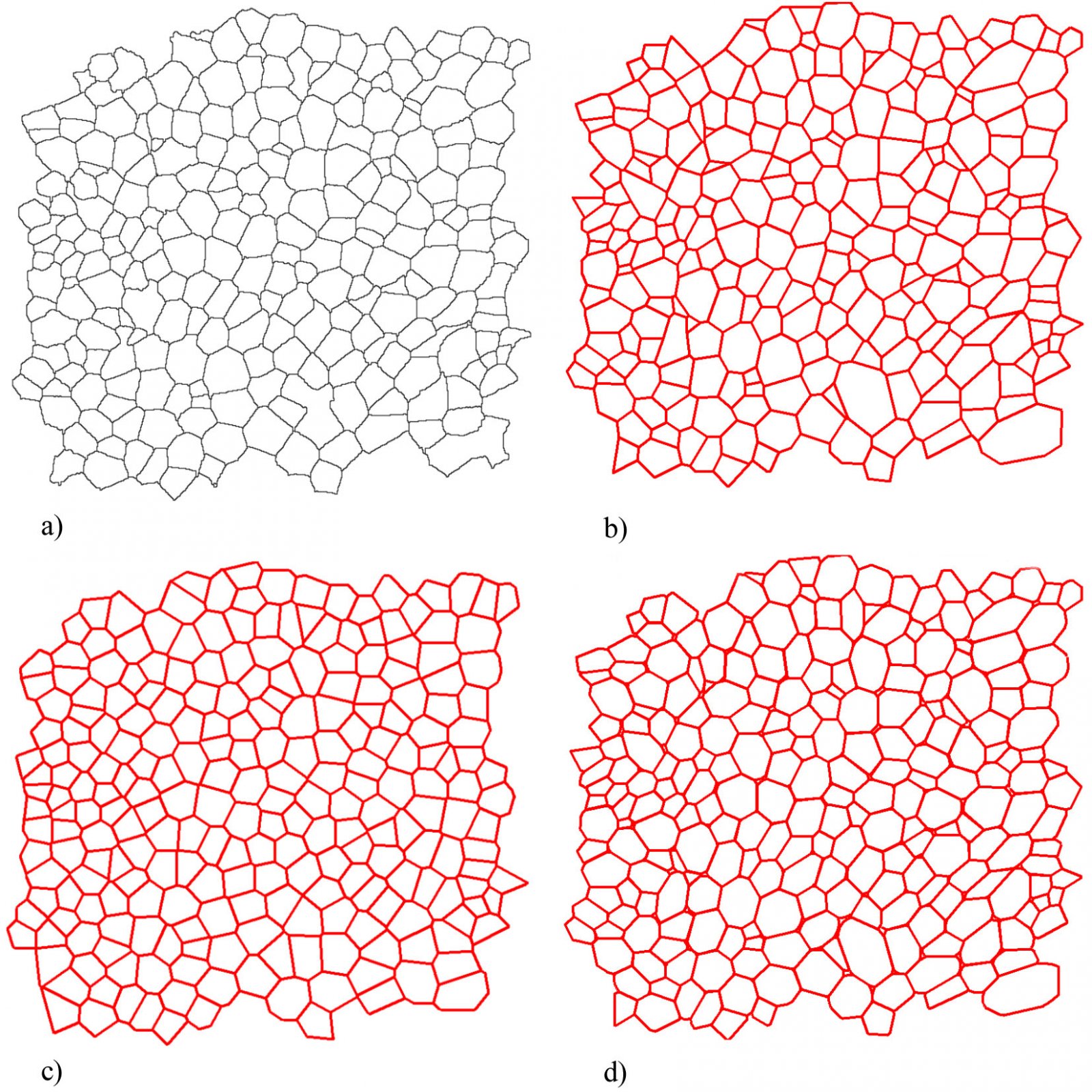
In the preliminary study three different methods for parameterisation of plant tissues were tested (Pieczywek et al., 2011).  All methods can be applied to images obtained with a confocal scanning laser microscope to create models for the simulation of the mechanical behaviour of biological cellular structures. Vectorisation, Voronoi tessellation and ellipse tessellation were tested. Potato tuber and carrot parenchyma were chosen as examples.

Modelowanie struktury tkanki

Jednym z kroków poprzedzających właściwą analizę MES jest utworzenie wirtualnej reprezentacji badanego obiektu. Wirtualny model zdefiniowany jest przez geometrię, właściwości materiałowe oraz warunki brzegowe reprezentujące oddziaływania zewnętrze oraz wewnętrzne. Istotne jest aby odwzorować modelowany system z możliwie największą dokładnością, przy jednoczesnym zachowaniu pewnych uroszczeń, umożliwiających przeprowadzenie obliczeń w rozsądnym czasie.

W badaniach wstępnych przetestowane zostały trzy różne metody parametryzacji struktury tkanki roślinnej (Pieczywek et al., 2011). Wszystkie metody zastosować można do obrazów mikroskopowych uzyskanych przy użyciu laserowego mikroskopu konfokalnego (CLSM), aby następnie utworzyć na ich podstawie wirtualne modele numeryczne struktur komórkowych. Testom poddano metodę wektoryzacji, teselacji eliptycznej, oraz teselacji Woronoja. Jako materiał badawczy wybrane zostały tkanki parenchymatyczne ziemniaka oraz marchwi.

Fig. 1. Vectorisation procedure: detection of a single cell boundary, detection of junction points,

connection of vertices and formation of a virtual cell.

Fig. 2. The process of creating a Voronoi diagram.

Fig. 3. The ellipse tessellation algorithm: fitting of ellipses, determination of the intersection points,

construction of “cutting lines”, the final model.

Fig. 4. Example of the parametrisation methods of the skeleton obtained from confocal scanning microscopy, a) original image of potato tissue, b) vectorisation, c) Voronoi tessellation, d) ellipse tessellation of the same structure.

Fig. 5. Performance of the parametrisation methods in reconstruction of irregularstructures: a) original image of carrot tissue, b) vectorisation, c) Voronoi tessellation, d) ellipse tessellation of the same structure.

Fig. 6. Video record of tensile test using the real onion epidermis tissue.

Fig. 7. Animation showing tensile test using the FEM model of onion epidermis tissue.

The models showed capabilities of simulating large strains with nonlinear behaviour and produced force-strain curves that closely matched the experimental data. The model revealed a significant influence of tissue structure on micromechanical properties and allowed for interpretation of the tensile test results (force-strain curves) with respect to changes occurring in the structure of the virtual tissue. This proved that qualitative improvement of the results obtained from FEM models of plant tissues is possible due to incorporation of the real microstructure.

Fig. 8. Experimental stress-strain curve for tensile test of onion epidermis tissue. E₁ – elasticity modulus in the first part of the curve, E₂ – modulus of elasticity in second linear part of curve (after transition to elasto-plastic deformation), σ_pl and ε_pl – stress and strain at the beginning of the transition phase, respectively.

Fig. 9. FEM models performance for three cell wall parameters: E_1exp, E_1mod – elasticity modulus in the first part of the curve, E_2exp, E_2mod – elastic modulus in second linear part of curve, σ_{pl exp}, σ_{pl mod} – stress and at the yielding point.

Future work

Simulations of fully 3D, automatic generated cellular structures.