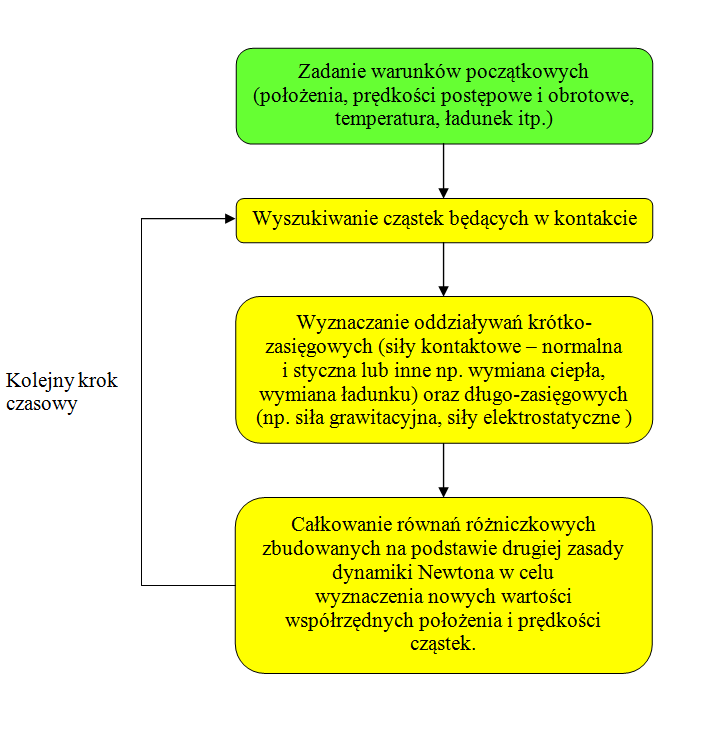
Metoda Elementów Dyskretnych

W zbiornikach przechowalniczych często istnieje konieczność umieszczania dodatkowych elementów wewnątrz złoża (czujniki, osłony podajników, rury odciążające itp.). Zaburzenia rozkładu naprężeń powodowane przez takie elementy mogą prowadzić w skrajnych przypadkach do uszkodzenia całej konstrukcji zbiornika. Rys. 1 przedstawia sposób, w jaki zmienia się charakter wypływu materiału sypkiego w modelowym silosie po zamontowaniu półki przy ścianie.

Większość  materiałów sypkich stanowi ośrodki niejednorodne pod względem wielkości cząstek, a stopień ich polidyspersyjności determinuje zachowanie materiałów w procesach mieszania i opróżniania zbiorników przemysłowych oraz reakcję materiałów poddanych obciążeniom podczas procesów tabletkowania, granulowania i innych.

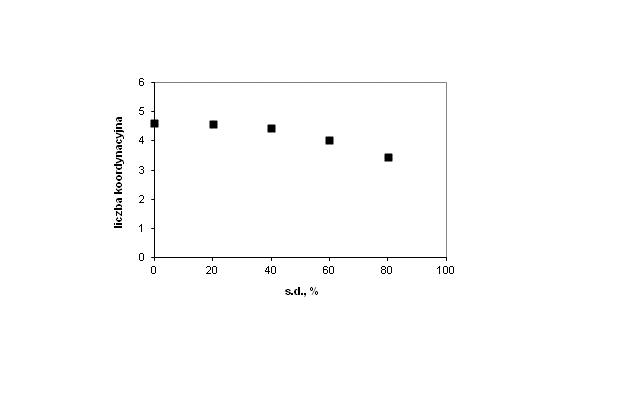
Zastosowanie Metody Elementów Dyskretnych umożliwiło przeprowadzenie badań nad materiałami o różnym stopniu niejednorodności wielkości cząstek, charakteryzującymi się różnymi rozkładami wymiarów granul (normalnym, przypadkowym i jednorodnym). Analiza geometrycznych i mechanicznych właściwości modelowanych ośrodków, poddanych testowi jednoosiowego ściskania (Rys. 1), wykazała niewielki wpływ rodzaju rozkładu wielkości cząstek na porowatość ośrodków rozdrobnionych oraz jego brak na mikro- i makromechaniczne właściwości próbek. Wraz ze wzrostem standardowego odchylenia średnicy sfer obserwowano wzrost porowatości złóż, ich sztywności oraz ilorazu naporu. Wzrost stopnia polidyspersyjności wielkości cząstek prowadził do spadku liczby koordynacyjnej w modelowanych próbkach (Rys. 2).